Pyrite – Damar, Murgul (Turquie).
Pseudo-icosaèdre {210}, {111}. © R. Warin.

PYRITE : PROPOS SUR LE PYRITOEDRE ET LE PSEUDO-ICOSAEDRE,
et les 5 Solides de Platon.

Déjà dans un passé lointain, vers – 300 av. J.C., PLATON réfléchissait aux choses du Monde. En philosophe éclairé, il analysait son environnement matériel qui le fascinait. Il détenait le savoir de l’époque, déjà bien développé. Les architectes du siècle de Périclès (5e siècle av. J.C.) étaient les dépositaires de notions avancées de la géométrie. Ils avaient construit les monuments de l’Acropole selon des proportions et des perspectives idoines. De nombreux philosophes de ce siècle d’or échafaudaient les premières théories qui contrôlent le monde matériel. Ainsi tous les matériaux constituant le monde seraient composés de quatre Éléments : la Terre, l'Eau, l'Air et le Feu. 

Platon désirait "établir des correspondances" entre ces 4 Eléments et les dimensions des choses (unité ou nombres ou lignes insécables, lignes ou longueurs, surfaces ou plans, volumes ou solides), figures (lignes insécables, lignes, triangle, pyramide) et nombres. Platon définissait 5 formes géométriques régulières, corrélées entre elles. Ce sont les 5 solides de Platon.

Ce qui est absolument indivisible, mais avec une position, est un point.

Ce qui est divisible selon une dimension est une ligne.

Ce qui est divisible selon deux dimensions est une surface.

Ce qui est absolument divisible en quantité et selon trois dimensions est un corps [un volume]. (Aristote, Métaphysique, Delta, 6, 1016 b).

Platon et les Penseurs de l’époque subséquente expliquaient le monde en utilisant la « Géométrie euclidienne ». Leurs notions du point, de la ligne, du plan et du volume s’appliquent aux minéraux. 

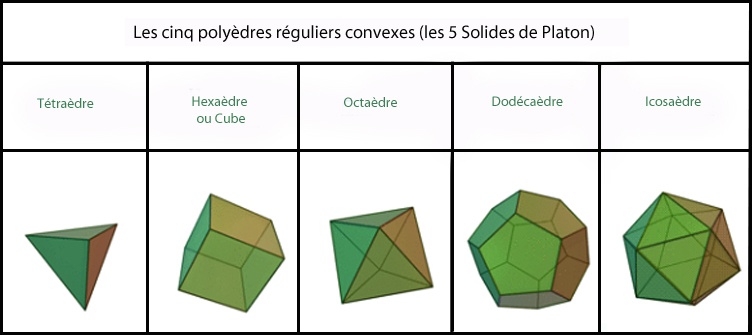
Les 5 Solides de Platon. Crédit : Wikipedia.

Parmi les 5 Solides de Platon, 3 sont possibles, car le dodécaèdre pentagonal et l’icosaèdre n’existent pas en cristallographie, car la symétrie pentagonale est interdite en minéralogie. Cette conclusion s’appuie sur un postulat, la matière minérale tend à occuper un espace minimum à l’état solide. Cependant, la symétrie d’ordre 5 existe dans le monde vivant et dans d’autres secteurs de la chimie.

Ainsi donc, la symétrie pentagonale n’existe pas dans le monde minéral (mais bien dans la Nature en général). Le collectionneur sait pourtant qu’il existe chez la pyrite, le pseudo-dodécaèdre pentagonal, correspondant à la troncature {210} du cube de pyrite. Ce solide n’est pas régulier, les arêtes des faces pentagonales étant dissemblables. Un dodécaèdre régulier est un solide composé de 12 faces. Le préfixe dodéca-, d'origine grecque, fait référence au nombre de faces. Un dodécaèdre régulier est l’un des solides de Platon composé de faces pentagonales, dont 3 se rejoignent à chaque sommet.

Pyrite sur hématite – Ile d’Elbe.
Pyritoèdre {210} © R. Warin.

Pyritoèdre théorique.

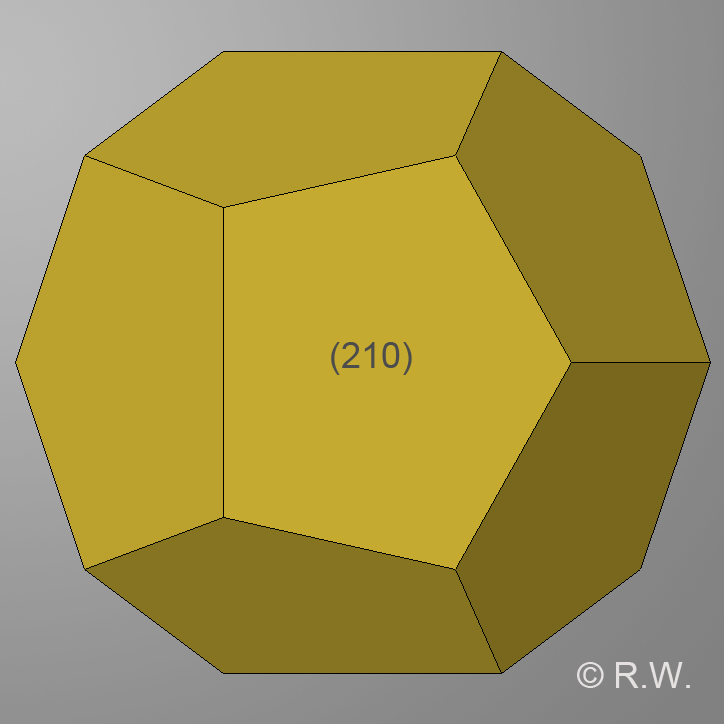
Le pyritoèdre de la pyrite n’est pas le dodécaèdre pentagonal régulier de Platon, alors qu’il existe une ressemblance troublante ente le 4e solide de Platon et le pseudo-dodécaèdre pentagonal de pyrite. Bien que cette forme de pyrite ne soit produite que par la seule troncature{210}, le solide naturel obtenu n’est pas « régulier ». En d’autres mots, ses arêtes n’ont pas toutes la même longueur (le raisonnement reste valable quand le pyritoèdre n’est pas naturellement déformé comme celui de la photo). Donc, les faces du pyritoèdre ne sont pas régulières, et forcément le pyritoèdre n'est pas non plus régulier.

C’est aussi par une astuce de combinaisons de formes différentes que le pseudo-icosaèdre de pyrite a pu cristalliser. Il en résulte une conséquence, ce pseudo-icosaèdre n’est pas aussi compact ni symétrique que le vrai, le 5e Solide de Platon.

Ainsi, bien que l’icosaèdre vrai (du grec είκοσι (eíkosi) « vingt » et εδρα (hédra) « siège, face » contienne 375 fois le rapport du nombre d’Or, ce Solide mythique n’est pas non plus utilisé par la Nature minérale. Celle-ci a des contraintes de symétrie qui ne peuvent s’adapter à la symétrie d’ordre 5 de l’icosaèdre. Pour obtenir un cristal dont le solide possède une forme approchée, il faut modifier les dimensions des faces et en conséquence changer les angles dièdres. Ainsi, les angles dièdres du pseudo-icosaèdre sont différents : les dièdres entre l’hexadièdre et l’octaèdre valent 39,2° tandis que ceux entre les faces de l’hexadièdre lui-même mesurent 53,1°. Quant à eux, les angles dièdres du vrai icosaèdre régulier valent tous 41,81°.

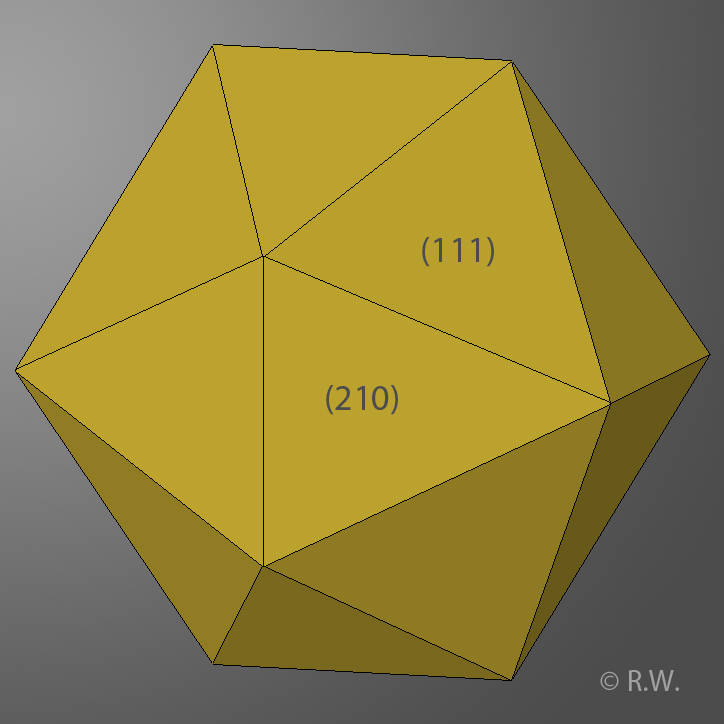
Modèle théorique de la combinaison du hexadièdre {210} (ou pyritoèdre) et de l’octaèdre {111}, 
en proportions pour former un pseudo-icosaèdre.

Ceci est une illustration de l’appartenance de la pyrite à la classe cristalline parahémiédrique du Système cubique. Cette classe (2/m 3) n’a pas toute la symétrie du cube (comme la possède la fluorite). Dans cette classe il n’y a que 4 axes ternaires, 3 axes binaires, 3 plans miroirs et 1 centre de symétrie.

En résumé, la pyrite peut prendre une morphologie pseudo-pentagonale selon les hasards des troncatures. Mais elle reste un minéral cubique, bien qu’elle ne possède pas tous les opérateurs possibles de symétrie. Les lignes parallèles de la pyrite triglyphe en attestent aussi.

Roger WARIN